class QTransform#

The QTransform class specifies 2D transformations of a coordinate system. More…

Synopsis#

Methods#

Static functions#

Note

This documentation may contain snippets that were automatically translated from C++ to Python. We always welcome contributions to the snippet translation. If you see an issue with the translation, you can also let us know by creating a ticket on https:/bugreports.qt.io/projects/PYSIDE

Detailed Description#

Warning

This section contains snippets that were automatically translated from C++ to Python and may contain errors.

A transformation specifies how to translate, scale, shear, rotate or project the coordinate system, and is typically used when rendering graphics.

A QTransform object can be built using the setMatrix() , scale() , rotate() , translate() and shear() functions. Alternatively, it can be built by applying basic matrix operations . The matrix can also be defined when constructed, and it can be reset to the identity matrix (the default) using the reset() function.

The QTransform class supports mapping of graphic primitives: A given point, line, polygon, region, or painter path can be mapped to the coordinate system defined by this matrix using the map() function. In case of a rectangle, its coordinates can be transformed using the mapRect() function. A rectangle can also be transformed into a polygon (mapped to the coordinate system defined by this matrix), using the mapToPolygon() function.

QTransform provides the isIdentity() function which returns true if the matrix is the identity matrix, and the isInvertible() function which returns true if the matrix is non-singular (i.e. AB = BA = I). The inverted() function returns an inverted copy of this matrix if it is invertible (otherwise it returns the identity matrix), and adjoint() returns the matrix’s classical adjoint. In addition, QTransform provides the determinant() function which returns the matrix’s determinant.

Finally, the QTransform class supports matrix multiplication, addition and subtraction, and objects of the class can be streamed as well as compared.

Rendering Graphics#

When rendering graphics, the matrix defines the transformations but the actual transformation is performed by the drawing routines in QPainter .

By default, QPainter operates on the associated device’s own coordinate system. The standard coordinate system of a QPaintDevice has its origin located at the top-left position. The x values increase to the right; y values increase downward. For a complete description, see the coordinate system documentation.

QPainter has functions to translate, scale, shear and rotate the coordinate system without using a QTransform . For example: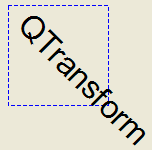

qtransform-simpletransformation1

 
def paintEvent(self, arg__0):

    painter = QPainter(self)
    painter.setPen(QPen(Qt.blue, 1, Qt.DashLine))
    painter.drawRect(0, 0, 100, 100)
    painter.rotate(45)
    painter.setFont(QFont("Helvetica", 24))
    painter.setPen(QPen(Qt.black, 1))
    painter.drawText(20, 10, "QTransform")

Although these functions are very convenient, it can be more efficient to build a QTransform and call setTransform() if you want to perform more than a single transform operation. For example: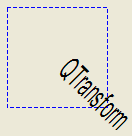

qtransform-combinedtransformation2

 
def paintEvent(self, arg__0):

    painter = QPainter(self)
    painter.setPen(QPen(Qt.blue, 1, Qt.DashLine))
    painter.drawRect(0, 0, 100, 100)
    transform = QTransform()
    transform.translate(50, 50)
    transform.rotate(45)
    transform.scale(0.5, 1.0)
    painter.setTransform(transform)
    painter.setFont(QFont("Helvetica", 24))
    painter.setPen(QPen(Qt.black, 1))
    painter.drawText(20, 10, "QTransform")

Basic Matrix Operations#

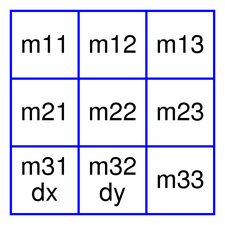
../../_images/qtransform-representation.png

A QTransform object contains a 3 x 3 matrix. The m31 (dx) and m32 (dy) elements specify horizontal and vertical translation. The m11 and m22 elements specify horizontal and vertical scaling. The m21 and m12 elements specify horizontal and vertical shearing. And finally, the m13 and m23 elements specify horizontal and vertical projection, with m33 as an additional projection factor.

QTransform transforms a point in the plane to another point using the following formulas:

x' = m11x + m21y + dx
y' = m22y + m12x + dy
if not isAffine():
    w' = m13x + m23y + m33
    x' /= w'
    y' /= w'

The point (x, y) is the original point, and (x’, y’) is the transformed point. (x’, y’) can be transformed back to (x, y) by performing the same operation on the inverted() matrix.

The various matrix elements can be set when constructing the matrix, or by using the setMatrix() function later on. They can also be manipulated using the translate() , rotate() , scale() and shear() convenience functions. The currently set values can be retrieved using the m11() , m12() , m13() , m21() , m22() , m23() , m31() , m32() , m33() , dx() and dy() functions.

Translation is the simplest transformation. Setting dx and dy will move the coordinate system dx units along the X axis and dy units along the Y axis. Scaling can be done by setting m11 and m22. For example, setting m11 to 2 and m22 to 1.5 will double the height and increase the width by 50%. The identity matrix has m11, m22, and m33 set to 1 (all others are set to 0) mapping a point to itself. Shearing is controlled by m12 and m21. Setting these elements to values different from zero will twist the coordinate system. Rotation is achieved by setting both the shearing factors and the scaling factors. Perspective transformation is achieved by setting both the projection factors and the scaling factors.

Combining Transforms#

Here’s the combined transformations example using basic matrix operations:

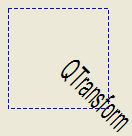
qtransform-combinedtransformation23

 
def paintEvent(self, arg__0):

    a = qDegreesToRadians(45.0)
    sina = sin(a)
    cosa = cos(a)
    scale = QTransform(0.5, 0, 0, 1.0, 0, 0)
    rotate = QTransform(cosa, sina, -sina, cosa, 0, 0)
    translate = QTransform(1, 0, 0, 1, 50.0, 50.0)
    transform = scale * rotate * translate
    painter = QPainter(self)
    painter.setPen(QPen(Qt.blue, 1, Qt.DashLine))
    painter.drawRect(0, 0, 100, 100)
    painter.setTransform(transform)
    painter.setFont(QFont("Helvetica", 24))
    painter.setPen(QPen(Qt.black, 1))
    painter.drawText(20, 10, "QTransform")

The combined transform first scales each operand, then rotates it, and finally translates it, just as in the order in which the product of its factors is written. This means the point to which the transforms are applied is implicitly multiplied on the left with the transform to its right.

Relation to Matrix Notation#

The matrix notation in QTransform is the transpose of a commonly-taught convention which represents transforms and points as matrices and vectors. That convention multiplies its matrix on the left and column vector to the right. In other words, when several transforms are applied to a point, the right-most matrix acts directly on the vector first. Then the next matrix to the left acts on the result of the first operation - and so on. As a result, that convention multiplies the matrices that make up a composite transform in the reverse of the order in QTransform , as you can see in Combining Transforms . Transposing the matrices, and combining them to the right of a row vector that represents the point, lets the matrices of transforms appear, in their product, in the order in which we think of the transforms being applied to the point.

See also

QPainter Coordinate System Affine Transformations ExampleTransformations Example

class TransformationType#

Constant

Description

QTransform.TxNone

QTransform.TxTranslate

QTransform.TxScale

QTransform.TxRotate

QTransform.TxShear

QTransform.TxProject
__init__(other)#
Parameters:

other – QTransform

__init__()

Constructs an identity matrix.

All elements are set to zero except m11 and m22 (specifying the scale) and m33 which are set to 1.

See also

reset()

__init__(h11, h12, h21, h22, dx, dy)
Parameters:

  • h11 – float

  • h12 – float

  • h21 – float

  • h22 – float

  • dx – float

  • dy – float

Constructs a matrix with the elements, m11, m12, m21, m22, dx and dy.

See also

setMatrix()

__init__(h11, h12, h13, h21, h22, h23, h31, h32, h33)
Parameters:

  • h11 – float

  • h12 – float

  • h13 – float

  • h21 – float

  • h22 – float

  • h23 – float

  • h31 – float

  • h32 – float

  • h33 – float

Constructs a matrix with the elements, m11, m12, m13, m21, m22, m23, m31, m32, m33.

See also

setMatrix()

__reduce__()#
Return type:

object

__repr__()#
Return type:

object

adjoint()#
Return type:

QTransform

Returns the adjoint of this matrix.

determinant()#
Return type:

float

Returns the matrix’s determinant.

dx()#
Return type:

float

Returns the horizontal translation factor.

See also

m31() translate() Basic Matrix Operations

dy()#
Return type:

float

Returns the vertical translation factor.

See also

translate() Basic Matrix Operations

static fromScale(dx, dy)#
Parameters:

  • dx – float

  • dy – float

Return type:

QTransform

Creates a matrix which corresponds to a scaling of sx horizontally and sy vertically. This is the same as QTransform() .scale(sx, sy) but slightly faster.

static fromTranslate(dx, dy)#
Parameters:

  • dx – float

  • dy – float

Return type:

QTransform

Creates a matrix which corresponds to a translation of dx along the x axis and dy along the y axis. This is the same as QTransform() .translate(dx, dy) but slightly faster.

inverted()#
Return type:

PyTuple

Returns an inverted copy of this matrix.

If the matrix is singular (not invertible), the returned matrix is the identity matrix. If invertible is valid (i.e. not 0), its value is set to true if the matrix is invertible, otherwise it is set to false.

See also

isInvertible()

isAffine()#
Return type:

bool

Returns true if the matrix represent an affine transformation, otherwise returns false.

isIdentity()#
Return type:

bool

Returns true if the matrix is the identity matrix, otherwise returns false.

See also

reset()

isInvertible()#
Return type:

bool

Returns true if the matrix is invertible, otherwise returns false.

See also

inverted()

isRotating()#
Return type:

bool

Returns true if the matrix represents some kind of a rotating transformation, otherwise returns false.

Note

A rotation transformation of 180 degrees and/or 360 degrees is treated as a scaling transformation.

See also

reset()

isScaling()#
Return type:

bool

Returns true if the matrix represents a scaling transformation, otherwise returns false.

See also

reset()

isTranslating()#
Return type:

bool

Returns true if the matrix represents a translating transformation, otherwise returns false.

See also

reset()

m11()#
Return type:

float

Returns the horizontal scaling factor.

See also

scale() Basic Matrix Operations

m12()#
Return type:

float

Returns the vertical shearing factor.

See also

shear() Basic Matrix Operations

m13()#
Return type:

float

Returns the horizontal projection factor.

See also

translate() Basic Matrix Operations

m21()#
Return type:

float

Returns the horizontal shearing factor.

See also

shear() Basic Matrix Operations

m22()#
Return type:

float

Returns the vertical scaling factor.

See also

scale() Basic Matrix Operations

m23()#
Return type:

float

Returns the vertical projection factor.

See also

translate() Basic Matrix Operations

m31()#
Return type:

float

Returns the horizontal translation factor.

See also

dx() translate() Basic Matrix Operations

m32()#
Return type:

float

Returns the vertical translation factor.

See also

dy() translate() Basic Matrix Operations

m33()#
Return type:

float

Returns the division factor.

See also

translate() Basic Matrix Operations

map(x, y)#
Parameters:

  • x – float

  • y – float

Return type:

PyObject

Warning

This section contains snippets that were automatically translated from C++ to Python and may contain errors.

Maps the given coordinates x and y into the coordinate system defined by this matrix. The resulting values are put in *``tx`` and *``ty``, respectively.

The coordinates are transformed using the following formulas:

x' = m11x + m21y + dx
y' = m22y + m12x + dy
if not isAffine():
    w' = m13x + m23y + m33
    x' /= w'
    y' /= w'

The point (x, y) is the original point, and (x’, y’) is the transformed point.

See also

Basic Matrix Operations

map(r)
Parameters:

r – QRegion

Return type:

QRegion

This is an overloaded function.

Creates and returns a QRegion object that is a copy of the given region, mapped into the coordinate system defined by this matrix.

Calling this method can be rather expensive if rotations or shearing are used.

map(a)
Parameters:

a – QPolygonF

Return type:

QPolygonF

This is an overloaded function.

Creates and returns a QPolygonF object that is a copy of the given polygon, mapped into the coordinate system defined by this matrix.

map(a)
Parameters:

a – QPolygon

Return type:

QPolygon

This is an overloaded function.

Creates and returns a QPolygon object that is a copy of the given polygon, mapped into the coordinate system defined by this matrix. Note that the transformed coordinates are rounded to the nearest integer.

map(p)
Parameters:

p – QPoint

Return type:

QPoint

This is an overloaded function.

Creates and returns a QPoint object that is a copy of the given point, mapped into the coordinate system defined by this matrix. Note that the transformed coordinates are rounded to the nearest integer.

map(p)
Parameters:

p – QPointF

Return type:

QPointF

This is an overloaded function.

Creates and returns a QPointF object that is a copy of the given point, p, mapped into the coordinate system defined by this matrix.

map(l)
Parameters:

l – QLine

Return type:

QLine

This is an overloaded function.

Creates and returns a QLineF object that is a copy of the given line, l, mapped into the coordinate system defined by this matrix.

map(l)
Parameters:

l – QLineF

Return type:

QLineF

This is an overloaded function.

Creates and returns a QLine object that is a copy of the given line, mapped into the coordinate system defined by this matrix. Note that the transformed coordinates are rounded to the nearest integer.

map(p)
Parameters:

p – QPainterPath

Return type:

QPainterPath

This is an overloaded function.

Creates and returns a QPainterPath object that is a copy of the given path, mapped into the coordinate system defined by this matrix.

mapRect(arg__1)#
Parameters:

arg__1 – QRect

Return type:

QRect

This is an overloaded function.

Creates and returns a QRect object that is a copy of the given rectangle, mapped into the coordinate system defined by this matrix. Note that the transformed coordinates are rounded to the nearest integer.

mapRect(arg__1)
Parameters:

arg__1 – QRectF

Return type:

QRectF

Warning

This section contains snippets that were automatically translated from C++ to Python and may contain errors.

Creates and returns a QRectF object that is a copy of the given rectangle, mapped into the coordinate system defined by this matrix.

The rectangle’s coordinates are transformed using the following formulas:

x' = m11x + m21y + dx
y' = m22y + m12x + dy
if not isAffine():
    w' = m13x + m23y + m33
    x' /= w'
    y' /= w'

If rotation or shearing has been specified, this function returns the bounding rectangle. To retrieve the exact region the given rectangle maps to, use the mapToPolygon() function instead.

See also

mapToPolygon() Basic Matrix Operations

mapToPolygon(r)#
Parameters:

r – QRect

Return type:

QPolygon

Warning

This section contains snippets that were automatically translated from C++ to Python and may contain errors.

Creates and returns a QPolygon representation of the given rectangle, mapped into the coordinate system defined by this matrix.

The rectangle’s coordinates are transformed using the following formulas:

x' = m11x + m21y + dx
y' = m22y + m12x + dy
if not isAffine():
    w' = m13x + m23y + m33
    x' /= w'
    y' /= w'

Polygons and rectangles behave slightly differently when transformed (due to integer rounding), so matrix.map(QPolygon(rectangle)) is not always the same as matrix.mapToPolygon(rectangle).

See also

mapRect() Basic Matrix Operations

__ne__(arg__1)#
Parameters:

arg__1 – QTransform

Return type:

bool

Returns true if this matrix is not equal to the given matrix, otherwise returns false.

__mul__(o)#
Parameters:

o – QTransform

Return type:

QTransform

Returns the result of multiplying this matrix by the given matrix.

Note that matrix multiplication is not commutative, i.e. a*b != b*a.

__mul__(n)
Parameters:

n – float

Return type:

QTransform

__imul__(arg__1)#
Parameters:

arg__1 – QTransform

Return type:

QTransform

This is an overloaded function.

Returns the result of multiplying this matrix by the given matrix.

__imul__(div)
Parameters:

div – float

Return type:

QTransform

This is an overloaded function.

Returns the result of performing an element-wise multiplication of this matrix with the given scalar.

__add__(n)#
Parameters:

n – float

Return type:

QTransform

__iadd__(div)#
Parameters:

div – float

Return type:

QTransform

This is an overloaded function.

Returns the matrix obtained by adding the given scalar to each element of this matrix.

__sub__(n)#
Parameters:

n – float

Return type:

QTransform

__isub__(div)#
Parameters:

div – float

Return type:

QTransform

This is an overloaded function.

Returns the matrix obtained by subtracting the given scalar from each element of this matrix.

__div__(n)#
Parameters:

n – float

Return type:

QTransform

operator/=(div)
Parameters:

div – float

Return type:

QTransform

This is an overloaded function.

Returns the result of performing an element-wise division of this matrix by the given scalar.

__eq__(arg__1)#
Parameters:

arg__1 – QTransform

Return type:

bool

Returns true if this matrix is equal to the given matrix, otherwise returns false.

static quadToQuad(arg__1, arg__2)#
Parameters:
Return type:

object

static quadToQuad(one, two, result)
Parameters:
Return type:

bool

Creates a transformation matrix, trans, that maps a four-sided polygon, one, to another four-sided polygon, two. Returns true if the transformation is possible; otherwise returns false.

This is a convenience method combining quadToSquare() and squareToQuad() methods. It allows the input quad to be transformed into any other quad.

static quadToSquare(arg__1)#
Parameters:

arg__1 – QPolygonF

Return type:

object

static quadToSquare(quad, result)
Parameters:
Return type:

bool

Creates a transformation matrix, trans, that maps a four-sided polygon, quad, to a unit square. Returns true if the transformation is constructed or false if such a transformation does not exist.

reset()#

Resets the matrix to an identity matrix, i.e. all elements are set to zero, except m11 and m22 (specifying the scale) and m33 which are set to 1.

See also

QTransform() isIdentity() Basic Matrix Operations

rotate(a[, axis=Qt.ZAxis])#
Parameters:

  • a – float

  • axis – Axis

Return type:

QTransform

This is an overloaded function.

Rotates the coordinate system counterclockwise by the given angle a about the specified axis at distance 1024.0 from the screen and returns a reference to the matrix.

Note that if you apply a QTransform to a point defined in widget coordinates, the direction of the rotation will be clockwise because the y-axis points downwards.

The angle is specified in degrees.

See also

setMatrix

rotate(a, axis, distanceToPlane)
Parameters:

  • a – float

  • axis – Axis

  • distanceToPlane – float

Return type:

QTransform

Rotates the coordinate system counterclockwise by the given angle a about the specified axis at distance distanceToPlane from the screen and returns a reference to the matrix.

Note that if you apply a QTransform to a point defined in widget coordinates, the direction of the rotation will be clockwise because the y-axis points downwards.

The angle is specified in degrees.

If distanceToPlane is zero, it will be ignored. This is suitable for implementing orthographic projections where the z coordinate should be dropped rather than projected.

See also

setMatrix()

rotateRadians(a, axis, distanceToPlane)#
Parameters:

  • a – float

  • axis – Axis

  • distanceToPlane – float

Return type:

QTransform

Rotates the coordinate system counterclockwise by the given angle a about the specified axis at distance distanceToPlane from the screen and returns a reference to the matrix.

Note that if you apply a QTransform to a point defined in widget coordinates, the direction of the rotation will be clockwise because the y-axis points downwards.

The angle is specified in radians.

If distanceToPlane is zero, it will be ignored. This is suitable for implementing orthographic projections where the z coordinate should be dropped rather than projected.

See also

setMatrix()

rotateRadians(a[, axis=Qt.ZAxis])
Parameters:

  • a – float

  • axis – Axis

Return type:

QTransform

This is an overloaded function.

Rotates the coordinate system counterclockwise by the given angle a about the specified axis at distance 1024.0 from the screen and returns a reference to the matrix.

Note that if you apply a QTransform to a point defined in widget coordinates, the direction of the rotation will be clockwise because the y-axis points downwards.

The angle is specified in radians.

See also

setMatrix()

scale(sx, sy)#
Parameters:

  • sx – float

  • sy – float

Return type:

QTransform

Scales the coordinate system by sx horizontally and sy vertically, and returns a reference to the matrix.

See also

setMatrix()

setMatrix(m11, m12, m13, m21, m22, m23, m31, m32, m33)#
Parameters:

  • m11 – float

  • m12 – float

  • m13 – float

  • m21 – float

  • m22 – float

  • m23 – float

  • m31 – float

  • m32 – float

  • m33 – float

Sets the matrix elements to the specified values, m11, m12, m13 m21, m22, m23 m31, m32 and m33. Note that this function replaces the previous values. QTransform provides the translate() , rotate() , scale() and shear() convenience functions to manipulate the various matrix elements based on the currently defined coordinate system.

See also

QTransform()

shear(sh, sv)#
Parameters:

  • sh – float

  • sv – float

Return type:

QTransform

Shears the coordinate system by sh horizontally and sv vertically, and returns a reference to the matrix.

See also

setMatrix()

static squareToQuad(arg__1)#
Parameters:

arg__1 – QPolygonF

Return type:

object

static squareToQuad(square, result)
Parameters:
Return type:

bool

Creates a transformation matrix, trans, that maps a unit square to a four-sided polygon, quad. Returns true if the transformation is constructed or false if such a transformation does not exist.

translate(dx, dy)#
Parameters:

  • dx – float

  • dy – float

Return type:

QTransform

Moves the coordinate system dx along the x axis and dy along the y axis, and returns a reference to the matrix.

See also

setMatrix()

transposed()#
Return type:

QTransform

Returns the transpose of this matrix.

type()#
Return type:

TransformationType

Returns the transformation type of this matrix.

The transformation type is the highest enumeration value capturing all of the matrix’s transformations. For example, if the matrix both scales and shears, the type would be TxShear, because TxShear has a higher enumeration value than TxScale.

Knowing the transformation type of a matrix is useful for optimization: you can often handle specific types more optimally than handling the generic case.